Skip to contents

Simulate Hierarchical Multinomial Logit Data

sim_hier_mnl.Rd

Generates simulated data suitable for testing hierarchical multinomial logit models, particularly those involving individual-specific covariates (Z) influencing coefficients (beta_i). Supports various functional forms for the Z-beta relationship and mixture models for residual heterogeneity.

Usage

sim_hier_mnl(
  nlgt = 300,
  nT = 10,
  p = 3,
  nz = 5,
  nXa = 2,
  nXd = 1,
  const = TRUE,
  z_dist_func = function(n, d) matrix(stats::runif(n * d, -1, 1), n, d),
  standardize_Z = TRUE,
  beta_func_type = "linear",
  beta_func_args = list(),
  ncomp = 1,
  mixture_comps = NULL,
  sigma_inv_diag = 1,
  Xa_dist_func = function(n, p, na) matrix(stats::runif(n * p * na, -1, 1), ncol = p *
    na),
  Xd_dist_func = function(n, nd) matrix(stats::rnorm(n * nd), ncol = nd),
  seed = NULL
)

Arguments

nlgt

Integer. Number of individuals or cross-sectional units.

nT

Integer. Number of choice observations per individual.

p

Integer. Number of choice alternatives (including outside option if any).

nz

Integer. Number of demographic/individual-specific variables in Z. If nz = 0, no Z matrix is generated, betabar_true is set to zero, and beta_func_type/beta_func_args are ignored.

nXa

Integer. Number of alternative-specific variables in X.

nXd

Integer. Number of choice-invariant variables in X (e.g., price).

const

Logical. Include p-1 intercepts in the model?

z_dist_func

Function. A function to generate the Z matrix. Must accept arguments n (nlgt) and d (nz) and return an n x d matrix. Default: function(n, d) matrix(runif(n*d, -1, 1), n, d).

standardize_Z

Logical. Standardize the generated Z matrix (mean 0, sd 1)?

beta_func_type

Character. Specifies the functional form mapping Z to the systematic component of beta (betabar_i). Ignored if nz = 0. Options:

  • "linear": Linear function betabar_i = Z_i %*% Delta. Requires Delta in beta_func_args.

  • "step": Step function based on one Z variable. Requires cutoff, beta_1, beta_2, Z_index in beta_func_args.

  • "friedman": Friedman benchmark function (modified) based on first 5 Z variables. Requires coef_index in beta_func_args to specify which coefficient it applies to (others are zero).

  • "custom": A user-defined function provided in beta_func_args$func.

beta_func_args

List. Arguments needed for the chosen beta_func_type. Ignored if nz = 0.

  • For "linear": list(Delta = matrix(runif(ncoef * nz), nrow=nz)). Delta is nz x ncoef.

  • For "step": list(cutoff = 0, beta_1 = rep(-1, ncoef), beta_2 = rep(1, ncoef), Z_index = 1). beta_1/beta_2 are vectors of length ncoef. Z_index is the column of Z to use.

  • For "friedman": list(coef_index = 1). nz must be >= 5. The function is applied to betabar_i[coef_index], others are 0.

  • For "custom": list(func = function(Zi) { ... }). The function must take a vector Zi (a row of Z) and return a vector betabar_i of length ncoef.

ncomp

Integer. Number of components in the normal mixture for residual heterogeneity (eps_i).

mixture_comps

List. Optional pre-specified mixture components. A list of length ncomp, where each element is list(mu = ..., rooti = ...). mu is the mean vector (length ncoef), rooti is the upper Cholesky factor of the inverse covariance matrix (ncoef x ncoef). If NULL, components are generated based on sigma_inv_diag.

sigma_inv_diag

Numeric. Diagonal value for the inverse covariance matrix (precision) of mixture components if mixture_comps is NULL. Assumes identity covariance scaled by this.

Xa_dist_func

Function. Function to generate alternative-specific variables Xa. Takes n (nT), p, na (nXa) and returns a matrix (usually n x (p*na) or similar structure expected by createX). Default: function(n, p, na) matrix(runif(n*p*na, -1, 1), ncol=p*na).

Xd_dist_func

Function. Function to generate choice-invariant variables Xd. Takes n (nT), nd (nXd) and returns an n x nd matrix. Default: function(n, nd) matrix(rnorm(n*nd), ncol=nd).

seed

Integer. Optional random seed for reproducibility.

Value

A list suitable for direct use as the Data argument in rhierMnlRwMixture, containing:

  • p: Number of alternatives.

  • lgtdata: List of length nlgt. Each element i is list(y=y_i, X=X_i, beta=beta_i, betabar=betabar_i).

  • Z: The nlgt x nz matrix of individual-specific covariates (standardized if requested). Additionally, the list contains true_values:

  • true_values$beta_true: nlgt x ncoef matrix of true beta_i.

  • true_values$betabar_true: nlgt x ncoef matrix of true betabar_i = f(Z_i).

  • true_values$true_params: List containing parameters used for generation (beta_func_type, beta_func_args, mixture_comps, pvec).

  • true_values$dimensions: List containing key dimensions used (p, nlgt, nT, nz, ncoef, etc.).

Examples

# Simple linear example
sim_data_linear <- sim_hier_mnl(nlgt = 50, nT = 5, p = 3, nz = 2, nXa = 1, nXd = 0,
                               beta_func_type = "linear", seed = 123)
plot(sim_data_linear$Z[,1], sim_data_linear$true_values$betabar_true[,1]) # Visualize linear


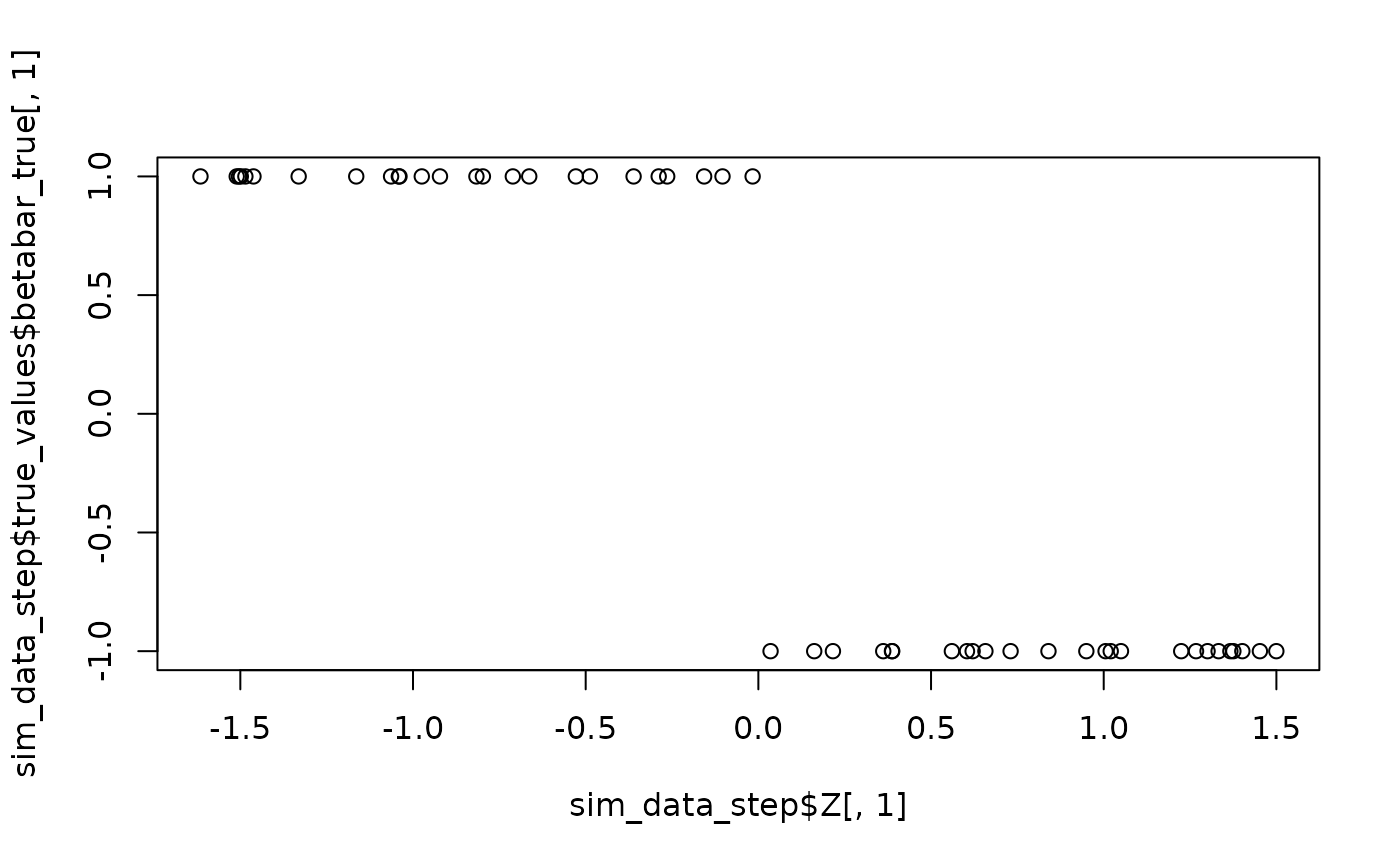
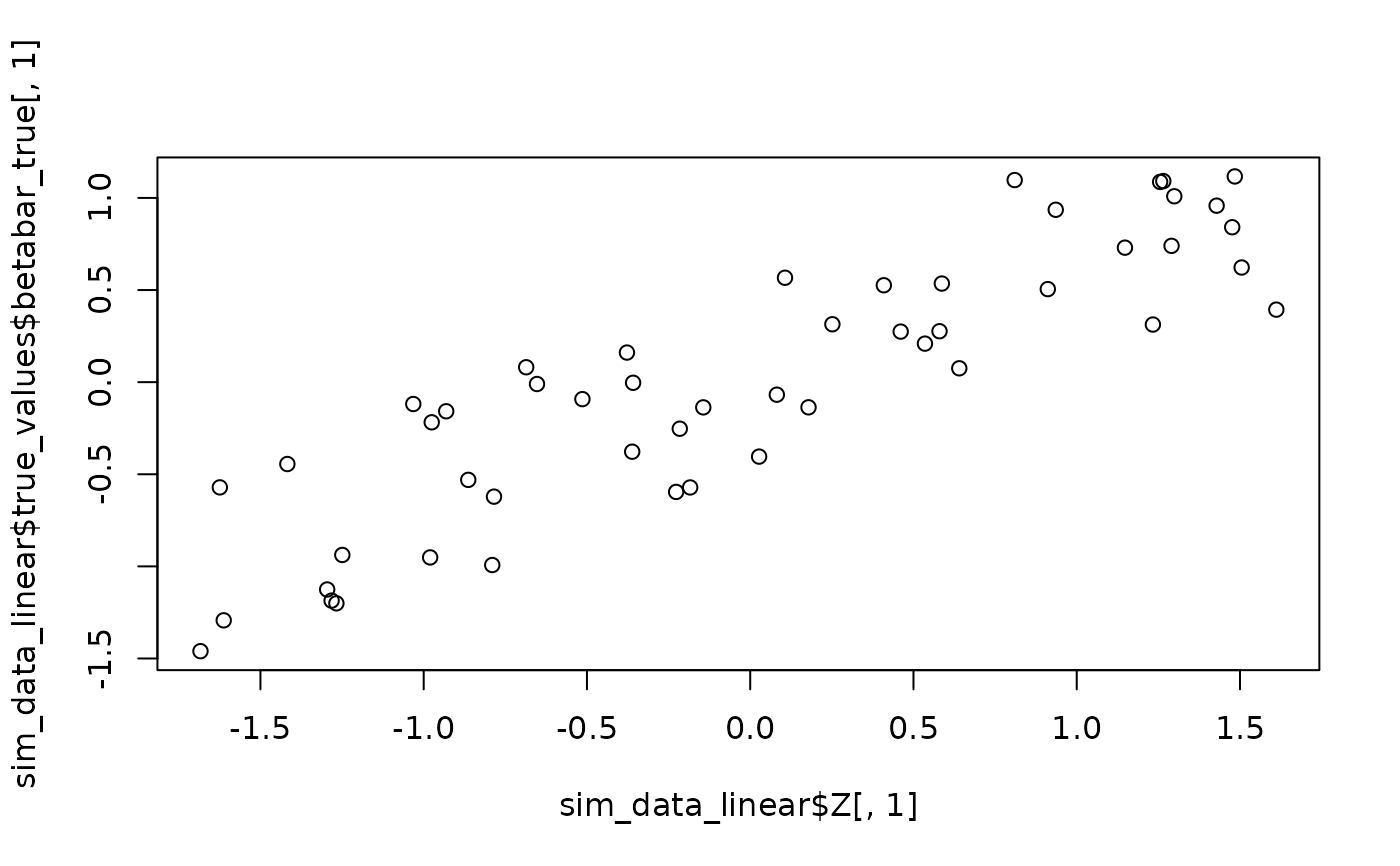# Step function example
sim_data_step <- sim_hier_mnl(nlgt = 50, nT = 5, p = 3, nz = 2, nXa = 1, nXd = 0,
                              beta_func_type = "step",
                              beta_func_args = list(Z_index = 1),
                              seed = 456)
plot(sim_data_step$Z[,1], sim_data_step$true_values$betabar_true[,1]) # Visualize step