Introduction
This article illustrates how ddml can complement the
highly popular did
package to compute group-time average treatment effects under a
conditional parallel trends assumption. The result is a
doubly-robust difference-in-difference estimator for staggered treatment
adoption designs that leverages machine learning and (short-)stacking to
flexibly control for covariates – or: difference-in-difference with
machine learning.
For an excellent introduction to differences-in-differences with multiple time periods, see also this article. For a detailed discussion of the relevant asymptotic theory for double/debiased machine learning difference-in-difference estimators see Chang (2020).
Estimation using did’s Default Estimator
For illustration, consider the data of Callaway and Sant’Anna (2020)
on county-level teen employment rates from 2003-2007 for additional
details. We are interested in the effect of treatment on the
log-employment rate lemp and assume that parallel trends
holds conditional on county population (lpop is the log of
county population).
# Load the did package
library(did)
set.seed(588239)
# Print the data
data(mpdta)
head(mpdta)
#> year countyreal lpop lemp first.treat treat
#> 866 2003 8001 5.896761 8.461469 2007 1
#> 841 2004 8001 5.896761 8.336870 2007 1
#> 842 2005 8001 5.896761 8.340217 2007 1
#> 819 2006 8001 5.896761 8.378161 2007 1
#> 827 2007 8001 5.896761 8.487352 2007 1
#> 937 2003 8019 2.232377 4.997212 2007 1By default, the group-time average treatment effect estimator of the
did package controls linearly for additional
covariates. (In particular, the propensity score is estimated using logistic
regression and the outcome reduced form is estimated via linear
regression). The below code snippet runs the default linear
specification (similar to this
article).
# Estimate group-time average treatment effects with covariates
attgt_lm <- att_gt(yname = "lemp",
gname = "first.treat",
idname = "countyreal",
tname = "year",
xformla = ~lpop,
data = mpdta)
# summarize the results
summary(attgt_lm)
#>
#> Call:
#> att_gt(yname = "lemp", tname = "year", idname = "countyreal",
#> gname = "first.treat", xformla = ~lpop, data = mpdta)
#>
#> Reference: Callaway, Brantly and Pedro H.C. Sant'Anna. "Difference-in-Differences with Multiple Time Periods." Journal of Econometrics, Vol. 225, No. 2, pp. 200-230, 2021. <https://doi.org/10.1016/j.jeconom.2020.12.001>, <https://arxiv.org/abs/1803.09015>
#>
#> Group-Time Average Treatment Effects:
#> Group Time ATT(g,t) Std. Error [95% Simult. Conf. Band]
#> 2004 2004 -0.0145 0.0231 -0.0757 0.0467
#> 2004 2005 -0.0764 0.0295 -0.1544 0.0016
#> 2004 2006 -0.1404 0.0382 -0.2417 -0.0392 *
#> 2004 2007 -0.1069 0.0338 -0.1963 -0.0175 *
#> 2006 2004 -0.0005 0.0226 -0.0603 0.0593
#> 2006 2005 -0.0062 0.0190 -0.0565 0.0441
#> 2006 2006 0.0010 0.0199 -0.0518 0.0537
#> 2006 2007 -0.0413 0.0207 -0.0962 0.0136
#> 2007 2004 0.0267 0.0145 -0.0116 0.0651
#> 2007 2005 -0.0046 0.0151 -0.0444 0.0353
#> 2007 2006 -0.0284 0.0177 -0.0752 0.0183
#> 2007 2007 -0.0288 0.0154 -0.0696 0.0121
#> ---
#> Signif. codes: `*' confidence band does not cover 0
#>
#> P-value for pre-test of parallel trends assumption: 0.23267
#> Control Group: Never Treated, Anticipation Periods: 0
#> Estimation Method: Doubly RobustThe did package offers visualization methods using
gglpot2:
ggdid(attgt_lm, ylim = c(-.4, .4))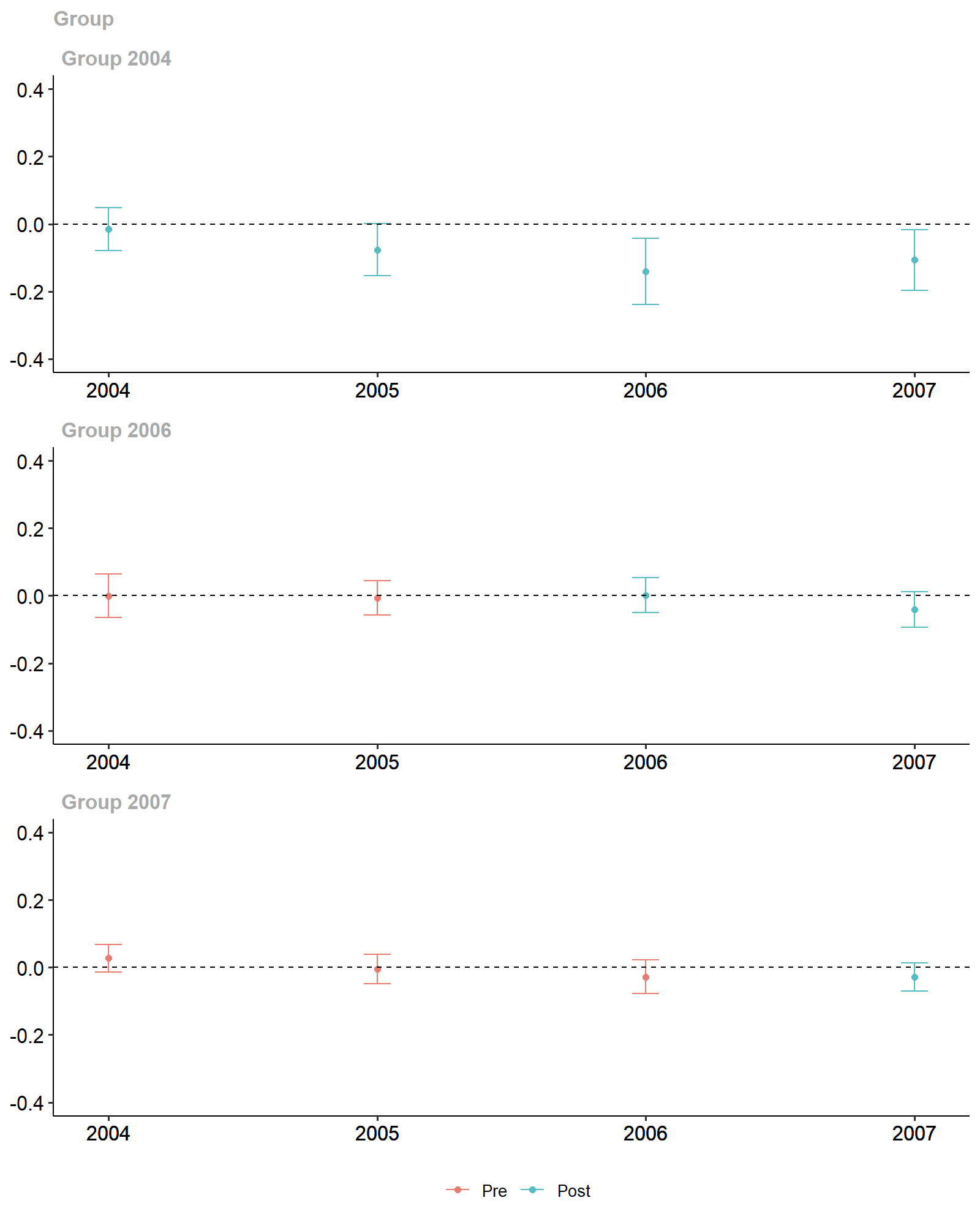
Diff-in-Diff Estimates.
Further, the group-time average treatment effects can easily be aggregated, for example, to estimate dynamic average treatment effects:
# aggregate the group-time average treatment effects
dyn_lm <- aggte(attgt_lm, type = "dynamic")
summary(dyn_lm)
#>
#> Call:
#> aggte(MP = attgt_lm, type = "dynamic")
#>
#> Reference: Callaway, Brantly and Pedro H.C. Sant'Anna. "Difference-in-Differences with Multiple Time Periods." Journal of Econometrics, Vol. 225, No. 2, pp. 200-230, 2021. <https://doi.org/10.1016/j.jeconom.2020.12.001>, <https://arxiv.org/abs/1803.09015>
#>
#>
#> Overall summary of ATT's based on event-study/dynamic aggregation:
#> ATT Std. Error [ 95% Conf. Int.]
#> -0.0804 0.0195 -0.1187 -0.042 *
#>
#>
#> Dynamic Effects:
#> Event time Estimate Std. Error [95% Simult. Conf. Band]
#> -3 0.0267 0.0135 -0.0085 0.0619
#> -2 -0.0036 0.0130 -0.0373 0.0301
#> -1 -0.0232 0.0151 -0.0624 0.0160
#> 0 -0.0211 0.0120 -0.0523 0.0102
#> 1 -0.0530 0.0166 -0.0961 -0.0099 *
#> 2 -0.1404 0.0371 -0.2368 -0.0441 *
#> 3 -0.1069 0.0352 -0.1982 -0.0156 *
#> ---
#> Signif. codes: `*' confidence band does not cover 0
#>
#> Control Group: Never Treated, Anticipation Periods: 0
#> Estimation Method: Doubly Robust
ggdid(dyn_lm, ylim = c(-.4, .4))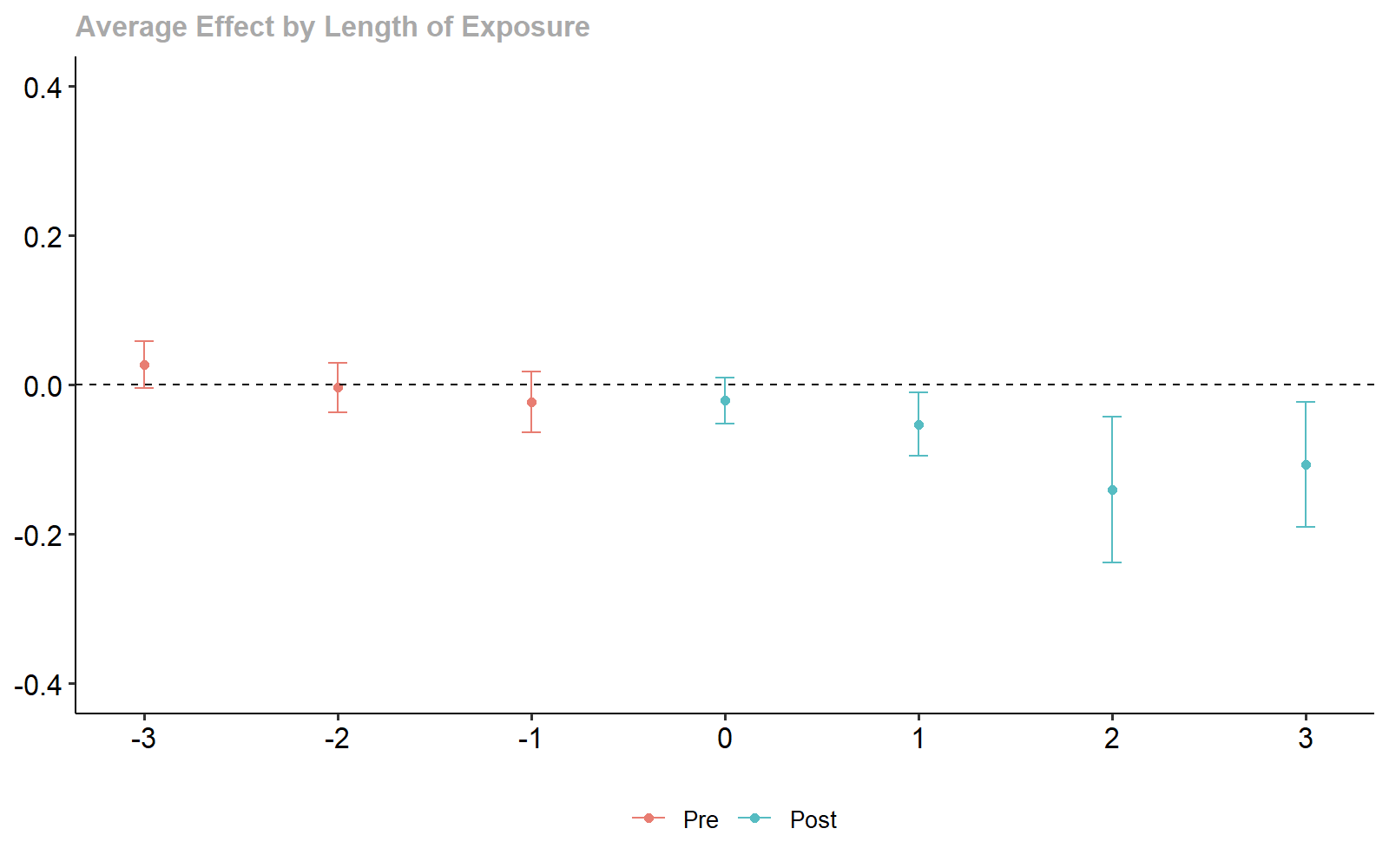
Dynamic Treatment Effect Estimates.
Contructing a xgboost-based Diff-in-Diff Estimator
Without additional parametric functional form assumptions on
the reduced form equations, it is not guaranteed that the
default att_gt estimator returns a convex combination of
causal effects. This is because linear predictors do not necessarily
correspond to the conditional expectation functions arising in the
doubly-robust score of the group-time average treatment effect. The
resulting misspecification error can then lead to negative weights in
the aggregation of individual-level treatment effects.
Fortunately, a convex combination of causal effects can be guaranteed (without parametric functional form assumptions) when using machine learning (nonparametric) reduced form estimators.
ddml facilitates the use of a large set of machine
learning reduced form estimators, including simultaneous considerations
of multiple estimators via (short-)stacking.
To use ddml estimators with the did
package, we can make use of the est_method argument of the
att_gt function (see also ?did::att_gt). It is
useful to construct this method in two steps:
- A simple wrapper for
ddml_attthat returns the objects needed byatt_gt - A second wrapper that hard-codes arguments passed to
ddml_att
This two-step approach allows for cleaner code when considering multiple ddml-based estimators (as we do in this article).
The below code-snippet constructs a simple estimation method following step 1:
# load the ddml package
library(ddml)
# write a general wrapper for ddml_att
ddml_did_method <- function(y1, y0, D, covariates, ...) {
# Compute difference in outcomes
delta_y <- y1 - y0
# Compute the ATT
att_fit <- ddml_att(y = delta_y, D = D, X = covariates, ...)
# Return results
inf.func <- att_fit$psi_b + att_fit$att * att_fit$psi_a
output <- list(ATT = att_fit$att, att.inf.func = inf.func)
return(output)
}#DDML_DID_METHODA potentially suitable machine learning reduced form estimator is
gradient tree boosting (see also ?mdl_xgboost). The below
code snippet completes the second wrapper by hard-coding both the
learner and its arguments. Here, we consider 10-fold cross-fitting with
a gradient tree boosting estimator (eta is the learning
rate, see also ?mdl_xgboost).
my_did_xgboost <- function(y1, y0, D, covariates, ...) {
# Hard-code learners
learners = list(what = mdl_xgboost,
args = list(nround = 500,
params = list(eta = 0.05, max_depth = 3),
early_stopping_rounds = 1))
learners_DX = learners
# Call the general ddml_did method w/ additional hard-coded arguments
ddml_did_method(y1, y0, D, covariates,
learners = learners,
learners_DX = learners_DX,
sample_folds = 10,
silent = TRUE)
}#MY_DID_XGBOOSTWe can now use the reduced form estimator my_did_xgboost
and pass it via the est_method argument:
# estimate group-time average treatment effects with ddml
attgt_xgboost <- att_gt(yname = "lemp",
gname = "first.treat",
idname = "countyreal",
tname = "year",
xformla = ~lpop,
data = mpdta,
est_method = my_did_xgboost)
#> Warning in trim_propensity_scores(m_X, trim, ensemble_type): : 207 propensity
#> scores were trimmed.
#> Warning in trim_propensity_scores(m_X, trim, ensemble_type): : 220 propensity
#> scores were trimmed.
#> Warning in trim_propensity_scores(m_X, trim, ensemble_type): : 208 propensity
#> scores were trimmed.
#> Warning in trim_propensity_scores(m_X, trim, ensemble_type): : 202 propensity
#> scores were trimmed.
#> Warning in trim_propensity_scores(m_X, trim, ensemble_type): : 48 propensity
#> scores were trimmed.
#> Warning in trim_propensity_scores(m_X, trim, ensemble_type): : 44 propensity
#> scores were trimmed.
#> Warning in trim_propensity_scores(m_X, trim, ensemble_type): : 49 propensity
#> scores were trimmed.
#> Warning in trim_propensity_scores(m_X, trim, ensemble_type): : 48 propensity
#> scores were trimmed.
# summarize the results
summary(attgt_xgboost)
#>
#> Call:
#> att_gt(yname = "lemp", tname = "year", idname = "countyreal",
#> gname = "first.treat", xformla = ~lpop, data = mpdta, est_method = my_did_xgboost)
#>
#> Reference: Callaway, Brantly and Pedro H.C. Sant'Anna. "Difference-in-Differences with Multiple Time Periods." Journal of Econometrics, Vol. 225, No. 2, pp. 200-230, 2021. <https://doi.org/10.1016/j.jeconom.2020.12.001>, <https://arxiv.org/abs/1803.09015>
#>
#> Group-Time Average Treatment Effects:
#> Group Time ATT(g,t) Std. Error [95% Simult. Conf. Band]
#> 2004 2004 0.1412 0.1138 -0.1427 0.4251
#> 2004 2005 0.1658 0.2354 -0.4213 0.7529
#> 2004 2006 -0.1373 0.3049 -0.8979 0.6232
#> 2004 2007 -0.1872 0.2251 -0.7486 0.3743
#> 2006 2004 0.0018 0.0519 -0.1276 0.1312
#> 2006 2005 -0.0162 0.0463 -0.1316 0.0993
#> 2006 2006 -0.0031 0.0431 -0.1105 0.1043
#> 2006 2007 0.0132 0.0661 -0.1517 0.1781
#> 2007 2004 -0.0648 0.1000 -0.3142 0.1847
#> 2007 2005 0.0458 0.0763 -0.1445 0.2362
#> 2007 2006 0.0381 0.1430 -0.3184 0.3947
#> 2007 2007 -0.0970 0.1165 -0.3876 0.1936
#> ---
#> Signif. codes: `*' confidence band does not cover 0
#>
#> P-value for pre-test of parallel trends assumption: 0.97672
#> Control Group: Never Treated, Anticipation Periods: 0
# plot the coefficients
ggdid(attgt_xgboost, ylim = c(-.4, .4))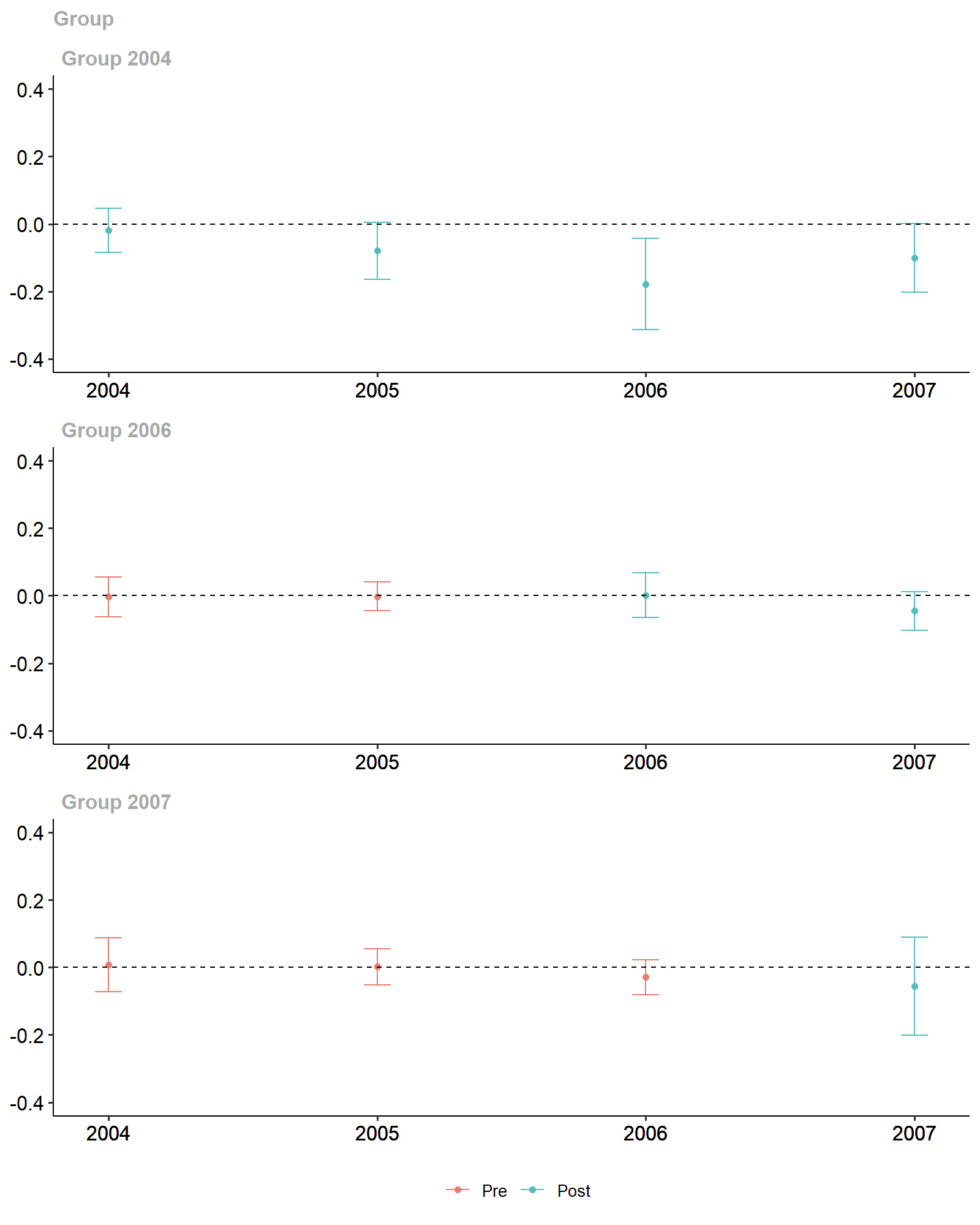
xgboost-based Diff-in-Diff Estimates.
Of course, use of the ddml-based reduced form estimator
still allows us to leverage the various other methods of the
did package, including the construction (and visualization
of) dynamic average treatment effects:
# aggregate the group-time average treatment effects
dyn_xgboost <- aggte(attgt_xgboost, type = "dynamic")
summary(dyn_xgboost)
#>
#> Call:
#> aggte(MP = attgt_xgboost, type = "dynamic")
#>
#> Reference: Callaway, Brantly and Pedro H.C. Sant'Anna. "Difference-in-Differences with Multiple Time Periods." Journal of Econometrics, Vol. 225, No. 2, pp. 200-230, 2021. <https://doi.org/10.1016/j.jeconom.2020.12.001>, <https://arxiv.org/abs/1803.09015>
#>
#>
#> Overall summary of ATT's based on event-study/dynamic aggregation:
#> ATT Std. Error [ 95% Conf. Int.]
#> -0.0782 0.1306 -0.3343 0.1779
#>
#>
#> Dynamic Effects:
#> Event time Estimate Std. Error [95% Simult. Conf. Band]
#> -3 -0.0648 0.1032 -0.2931 0.1635
#> -2 0.0355 0.0620 -0.1016 0.1727
#> -1 0.0254 0.1065 -0.2101 0.2610
#> 0 -0.0524 0.0841 -0.2384 0.1336
#> 1 0.0641 0.0854 -0.1247 0.2528
#> 2 -0.1373 0.3137 -0.8310 0.5564
#> 3 -0.1872 0.2189 -0.6711 0.2968
#> ---
#> Signif. codes: `*' confidence band does not cover 0
#>
#> Control Group: Never Treated, Anticipation Periods: 0
ggdid(dyn_xgboost, ylim = c(-.4, .4))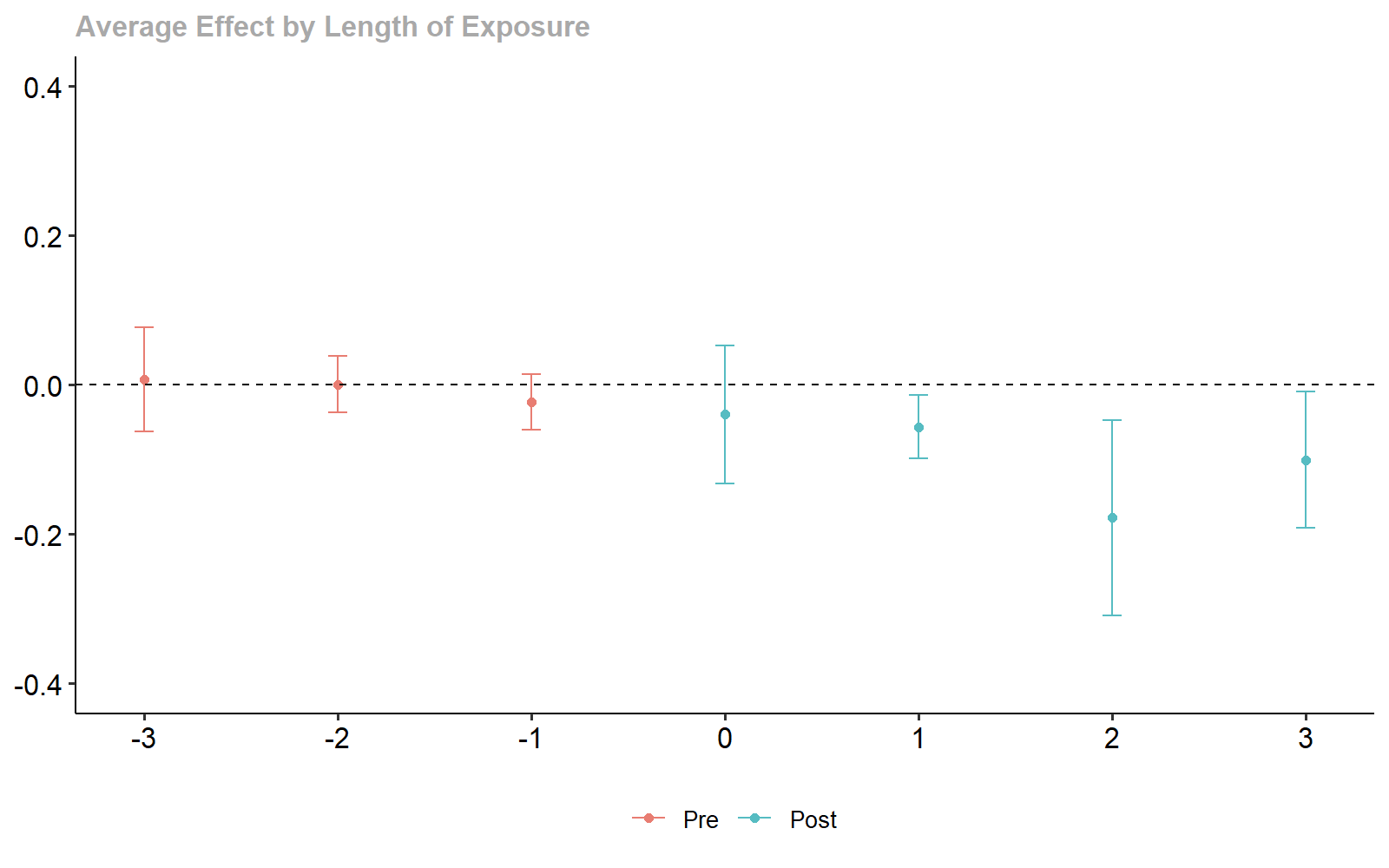
xgboost-based Dynamic Treatment Effect Estimates.
The gradient tree boosting-based ATT estimate is only slightly
different from the ATT estimate using the linear estimator of the
did package, however, it is statistically
insignificant.
Given these two coefficients, is there a good reason to choose one over the other?
It is ex-ante difficult to trade-off the potential bias from
misspecification that the linear estimator suffers from with the
potential bias from estimation error that the gradient tree boosting
estimator may suffer from. ddml allows to resolve this
conflict in a data-driven manner by simultaneous consideration of
multiple machine learners via (short-)stacking. We turn to this in the
next section.
Contructing a Shortstacking-based Diff-in-Diff Estimator
Instead of considering just a single machine learner – that may or may not be suitable for the given application – we can leverage (short-)stacking and simultaneously consider multiple machine learners. As in other settings, this substantially increases robustness to the underlying structure of the data.
We construct a new wrapper for our ddml_did_method that
hard-codes different reduced form estimators:
- linear or logistic regression
- gradient tree boosting with more and less regularization
- random forests with more and less regularization
The reduced form estimators are then optimally combined via
non-negative least squares. Note that this specification also includes
the linear control specifications considered by the default
did learner, ensuring that machine learners are not
spuriously selected. We leverage shortstacking to reduce computational
time (see also vignette("stacking")).
my_did_stacking <- function(y1, y0, D, covariates, ...) {
# Hard-code learners for outcome reduced-form
learners = list(list(fun = ols),
list(fun = mdl_xgboost,
args = list(nround = 500,
params = list(eta = 0.05, max_depth = 1),
early_stopping_rounds = 1)),
list(fun = mdl_xgboost,
args = list(nround = 500,
params = list(eta = 0.05, max_depth = 3),
early_stopping_rounds = 1)),
list(fun = mdl_ranger,
args = list(num.trees = 1000,
max.depth = 1)),
list(fun = mdl_ranger,
args = list(num.trees = 1000,
max.depth = 20)))
# Hard-code learners for treatment reduced-form
learners_DX = list(list(fun = mdl_glm),
list(fun = mdl_xgboost,
args = list(nround = 500,
params = list(eta = 0.05, max_depth = 1),
early_stopping_rounds = 1)),
list(fun = mdl_xgboost,
args = list(nround = 500,
params = list(eta = 0.05, max_depth = 3),
early_stopping_rounds = 1)),
list(fun = mdl_ranger,
args = list(num.trees = 1000,
max.depth = 1)),
list(fun = mdl_ranger,
args = list(num.trees = 1000,
max.depth = 20)))
# Call the general ddml_did method w/ additional hard-coded arguments
ddml_did_method(y1, y0, D, covariates,
learners = learners,
learners_DX = learners_DX,
sample_folds = 10,
ensemble_type = "nnls",
shortstack = TRUE,
silent = TRUE)
}#MY_DID_STACKINGFinally, we recompute the group-time average treatment effects using our shortstacking estimator:
# estimate group-time average treatment effects with ddml
attgt_stacking <- att_gt(yname = "lemp",
gname = "first.treat",
idname = "countyreal",
tname = "year",
xformla = ~lpop ,
data = mpdta,
est_method = my_did_stacking)
#> Warning in trim_propensity_scores(m_X, trim, ensemble_type): 2 propensity
#> scores were trimmed.
#> Warning in trim_propensity_scores(m_X, trim, ensemble_type): 1 propensity
#> scores were trimmed.
#> Warning in trim_propensity_scores(m_X, trim, ensemble_type): 2 propensity
#> scores were trimmed.
#> Warning in trim_propensity_scores(m_X, trim, ensemble_type): 2 propensity
#> scores were trimmed.
# summarize the results
summary(attgt_stacking)
#>
#> Call:
#> att_gt(yname = "lemp", tname = "year", idname = "countyreal",
#> gname = "first.treat", xformla = ~lpop, data = mpdta, est_method = my_did_stacking)
#>
#> Reference: Callaway, Brantly and Pedro H.C. Sant'Anna. "Difference-in-Differences with Multiple Time Periods." Journal of Econometrics, Vol. 225, No. 2, pp. 200-230, 2021. <https://doi.org/10.1016/j.jeconom.2020.12.001>, <https://arxiv.org/abs/1803.09015>
#>
#> Group-Time Average Treatment Effects:
#> Group Time ATT(g,t) Std. Error [95% Simult. Conf. Band]
#> 2004 2004 -0.0143 0.0224 -0.0748 0.0461
#> 2004 2005 -0.0761 0.0296 -0.1558 0.0036
#> 2004 2006 -0.1372 0.0371 -0.2370 -0.0374 *
#> 2004 2007 -0.1062 0.0318 -0.1918 -0.0205 *
#> 2006 2004 -0.0020 0.0214 -0.0595 0.0554
#> 2006 2005 -0.0061 0.0199 -0.0596 0.0475
#> 2006 2006 0.0016 0.0184 -0.0478 0.0510
#> 2006 2007 -0.0432 0.0203 -0.0978 0.0113
#> 2007 2004 0.0263 0.0145 -0.0127 0.0653
#> 2007 2005 -0.0036 0.0162 -0.0474 0.0401
#> 2007 2006 -0.0276 0.0193 -0.0794 0.0243
#> 2007 2007 -0.0275 0.0173 -0.0740 0.0189
#> ---
#> Signif. codes: `*' confidence band does not cover 0
#>
#> P-value for pre-test of parallel trends assumption: 0.24863
#> Control Group: Never Treated, Anticipation Periods: 0
# plot the coefficients
ggdid(attgt_stacking, ylim = c(-.4, .4))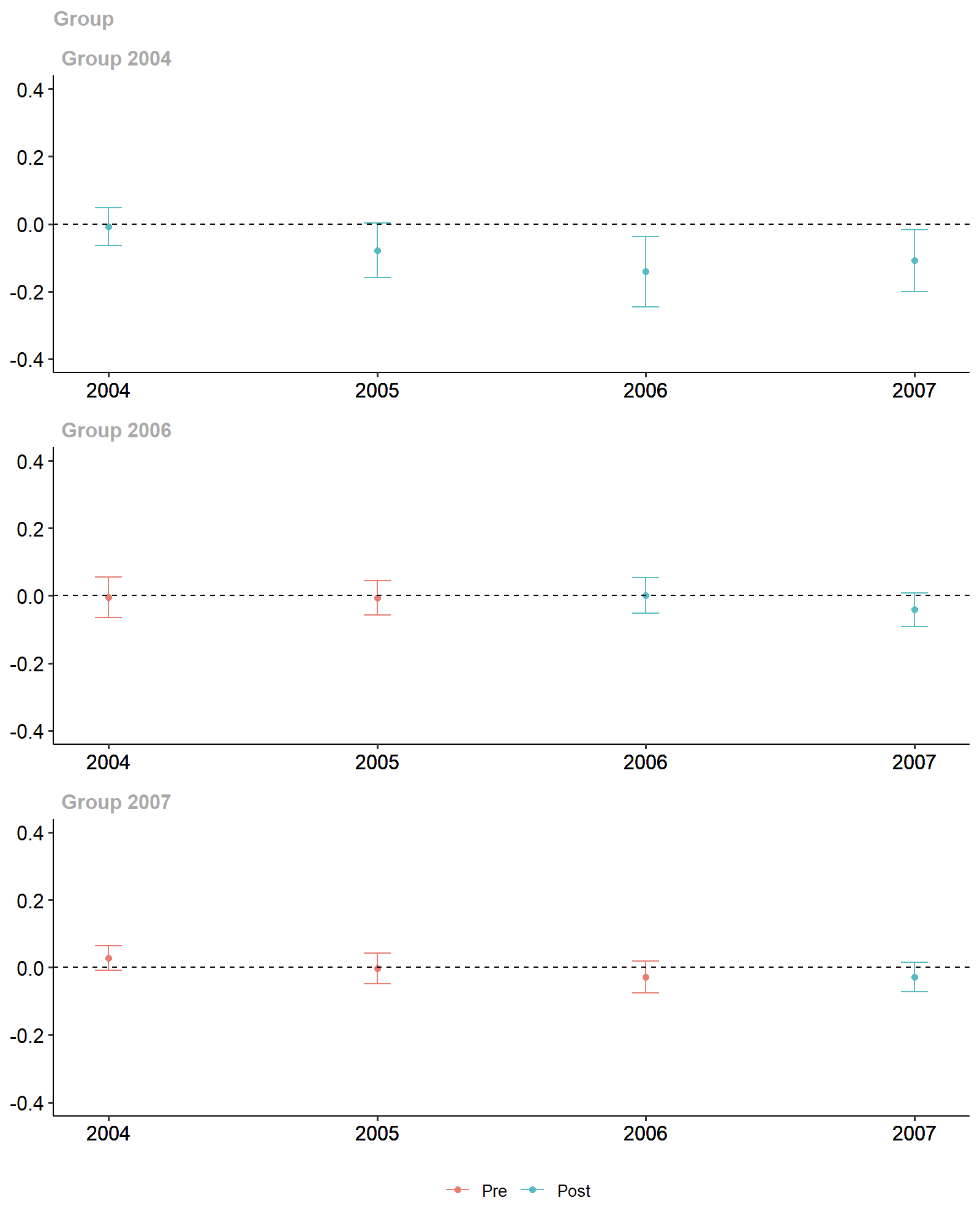
Stacking-based Diff-in-Diff Estimates.
The results are largely similar to those of the default linear
estimator of the did package, suggesting that the linear
approximation of the reduced forms is sufficiently accurate. (Of course
we didn’t know that before – now, at least, we can sleep easy!)
Other settings, in particular settings with multiple control variables, may show starker difference in the final estimates.
# aggregate the group-time average treatment effects
dyn_stacking <- aggte(attgt_stacking, type = "dynamic")
summary(dyn_stacking)
#>
#> Call:
#> aggte(MP = attgt_stacking, type = "dynamic")
#>
#> Reference: Callaway, Brantly and Pedro H.C. Sant'Anna. "Difference-in-Differences with Multiple Time Periods." Journal of Econometrics, Vol. 225, No. 2, pp. 200-230, 2021. <https://doi.org/10.1016/j.jeconom.2020.12.001>, <https://arxiv.org/abs/1803.09015>
#>
#>
#> Overall summary of ATT's based on event-study/dynamic aggregation:
#> ATT Std. Error [ 95% Conf. Int.]
#> -0.0794 0.0202 -0.1189 -0.0399 *
#>
#>
#> Dynamic Effects:
#> Event time Estimate Std. Error [95% Simult. Conf. Band]
#> -3 0.0263 0.0144 -0.0111 0.0638
#> -2 -0.0033 0.0132 -0.0375 0.0310
#> -1 -0.0225 0.0148 -0.0611 0.0160
#> 0 -0.0200 0.0110 -0.0487 0.0086
#> 1 -0.0542 0.0164 -0.0969 -0.0114 *
#> 2 -0.1372 0.0402 -0.2419 -0.0325 *
#> 3 -0.1062 0.0341 -0.1949 -0.0175 *
#> ---
#> Signif. codes: `*' confidence band does not cover 0
#>
#> Control Group: Never Treated, Anticipation Periods: 0
ggdid(dyn_stacking, ylim = c(-.4, .4))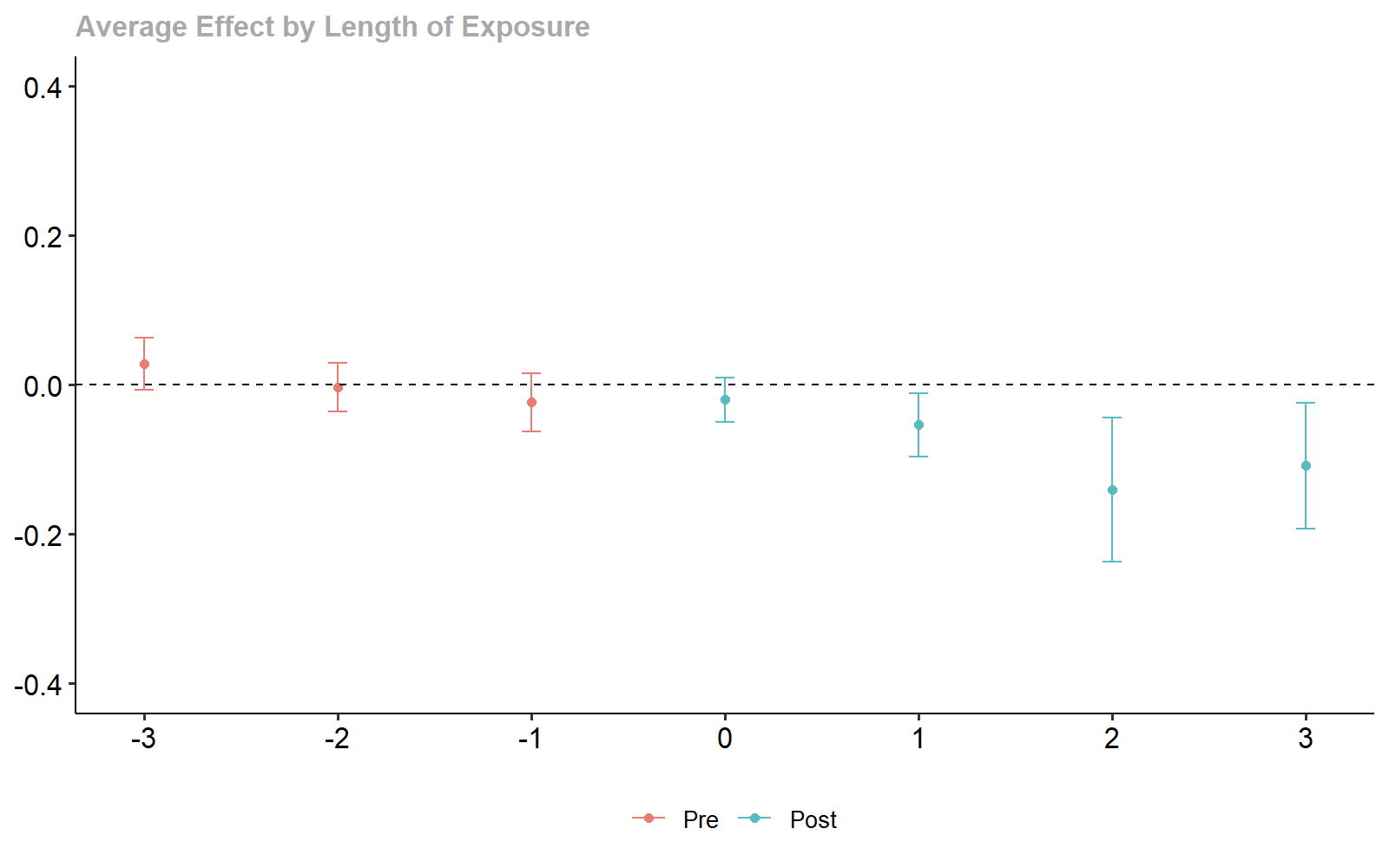
Stacking-based Dynamic Treatment Effect Estimates.
References
Callaway B, Sant’Anna P (2021). “Difference-in-differences with multiple time periods.” Journal of Econometrics, 200-230.
Callaway B, Sant’Anna P (2021). “did: Difference in Differences.” R package version 2.1.2, https://bcallaway11.github.io/did/.
Chang NC (2020). “Double/debiased machine learning for difference-in-difference models.” The Econometrics Journal, 177-191.